續上一篇機器學習 挑戰 - Day 2，
我們今天繼續詳細研究一下如何套用 ARIMA 來預測BTC的價格。

Auto-Regressive Integrated Moving Average (ARIMA)
用於時間序列分析預測的一般統計模型。由3個組成部分組成：AR + I + MA（p，d，q）

**Step 3 算出 p 以及q **
要算出p以及q，我們可以用以下的原則：

• 如果 PACF 圖在滯後 p 有顯著的尖峰，但沒有超過；而 ACF 圖則衰減得更緩慢 ----> ARIMA (p,d,0) 模型
• 如果 ACF 圖在滯後 q 有顯著的尖峰，但沒有超過；而 PACF 圖則衰減得更緩慢----> ARIMA(0,d,q) 模型

以PACF 以及ACF來看的話，ACF的波動是慢慢地減少的，而PACF就在lag 2.5前有個尖峰，因次，我推測應該要用ARIMA (p,d,0) 模型。p值則是在1跟2.5之間。由於ARIMA模塊只能用整數，我決定用2來當p值

Step 4 把預測畫上去
雖然數據不穩定所以預測不會那麼地準確但我還是希望能驗證一下我選數值準不準確。
因此我決定測試4種pdq：

1. ARIMA(2,0,0)
2. ARIMA(0,0,2)
3. ARIMA(2,0,1)
4. ARIMA(1,0,2)

再次地用statsmodels來導入ARIMA:

from statsmodels.tsa.arima.model import ARIMA

model1 = ARIMA(df_train, order=(2,0,0)) #p,d,0
model_fit1 = model1.fit()

model2 = ARIMA(df_train, order=(0,0,2)) #0,d,q
model_fit2 = model2.fit()

model3 = ARIMA(df_train, order=(2,0,1)) #p,d,q
model_fit3 = model3.fit()

model4 = ARIMA(df_train, order=(1,0,2)) #p,d,q
model_fit4 = model4.fit()

forecast_test1 = model_fit1.forecast(len(df_test)) 
forecast_test2 = model_fit2.forecast(len(df_test)) 
forecast_test3 = model_fit3.forecast(len(df_test)) 
forecast_test4 = model_fit4.forecast(len(df_test)) 

df2['forecast_manual1'] = [None] *len(df_train) + list(forecast_test1)
df2['forecast_manual2'] = [None] *len(df_train) + list(forecast_test2)
df2['forecast_manual3'] = [None] *len(df_train) + list(forecast_test3)
df2['forecast_manual4'] = [None] *len(df_train) + list(forecast_test4)

df2.plot()

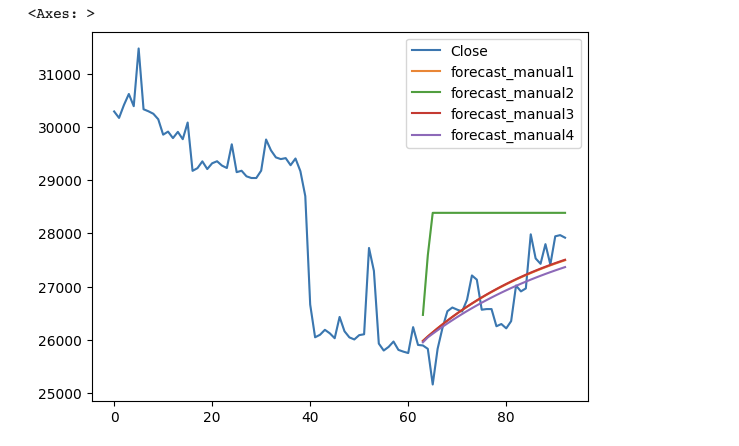
如上圖，可以看到綠線ARIMA(0,0,2)是離真實數據差得最遠的， 而紅色ARIMA(2,0,0)以及橘色線ARIMA(2,0,1)是最接近的。 這跟我選的p值=2，d值=0,q值＝0 是符合的。

在此，我也想確認一下數據的有沒有显著的残差(residuals)。

import matplotlib.pyplot as plt

# if the model is good, then the residuals should look like white noise
residuals = model_fit3.resid[1:] 

acf_res = plot_acf(residuals)
pacf_res = plot_pacf(residuals)

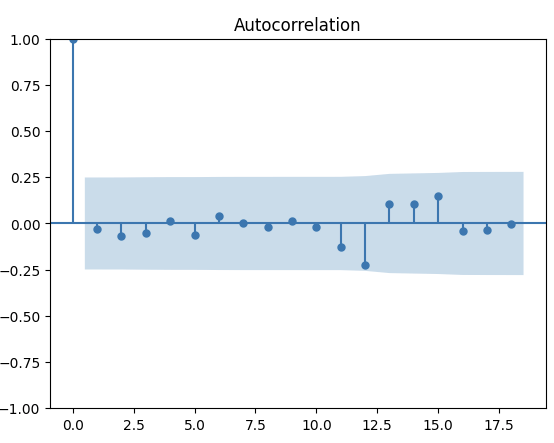
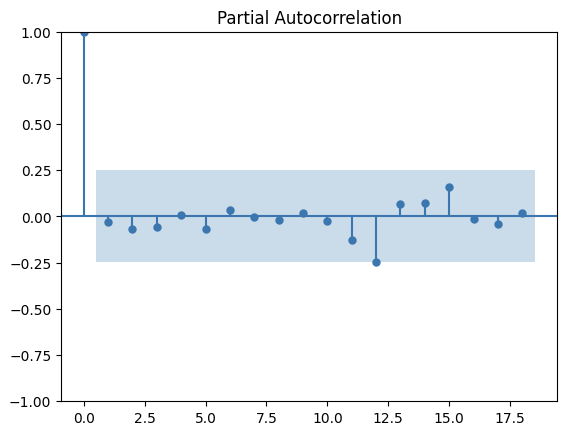
上圖顯示沒有波動是在藍色外面的，這也意味著沒有重要的残差。

我自已對ARIMA的感想就是:會要變成看得懂線圖以及理解統計學的基本理論才可以理解ARIMA是如何用歷史數據以及不同的時間序列來預測為來。 感覺是適合用來預測有季節性或歷史會重複的數據。

下一篇我想要研究一下用tensorflow.keras.models的LSTM。請拭目以待。

對 dbt 或 data 有興趣？歡迎加入 dbt community 到 #local-taipei 找我們，也有實體 Meetup 請到 dbt Taipei Meetup 報名參加
Ref:

https://levelup.gitconnected.com/20-pandas-functions-for-80-of-your-data-science-tasks-b610c8bfe63c